対応のある2群のノンパラメトリック検定:表計算ソフトで行うWilcoxonの検定 Wilcoxonの検定は対応ある2群のノンパラメトリック検定 の一つです。 次のようなデータの検定に利用します。 ・アンケートやVASで計測したデータの順位は正しいという仮定を利用今日は、ウィルコクソンの順位和検定について! ノンパラメトリックな検定では一番目にするのではないかと思います。 でも、ノンパラメトリックってそもそも何だろう? マンホイットニーのu検定と何が違うの? t検定と何が違うの? 何で検定の名前に順位ってついてるの?カイ二乗 (χ2)検定をする Excelの使い方 ExcelでCHISQTEST関数を利用して、カイ二乗 (χ2)検定をする手順を紹介します。
マン ホイットニー の U 検定 Mann
マンホイットニーのu検定 エクセル 関数
マンホイットニーのu検定 エクセル 関数-1531 UTest UTestは母集団に属する平均μと標本標準偏差s、標本平均xm、平均値の標準偏差sm (=s/√n)により、 U= (xmμ)/ (s/√n)= (xmμ)/sm で計算される。 UとUα (正規分布曲線の確率面積表のt値) を比較して合格判定する。 (例)有意水準5%として、μ=45、s=5、xm=49がn=10回観測の一つの集合であるか(帰無仮説)、UTestで判定せよ。 (解) U= (xm例えば、1位のデータが1個、2位のデータが2個ある場合、2位のデータには2位と3位の平均から25位を割り当てます。 次に2標本それぞれのデータの順位和( \ (R_1,\ R_2\) )とサンプルサイズ( \ (n_1,\ n_2\) )から、統計量( \ (U_1,\ U_2\) )を求め、どちらか小さい方を検定統計量 \ (U\) とします。 両側検定のみ行い、\ (U\) が統計数値表の有意水準5%と1%の棄却限界値以下




T 検定メインページ Ultrabem トップページ
MannWhitney(マン・ホイットニー)のU検定は、正規分布に従っておらず、比較対象が異なる集団であれば用いることができます。 臨床研究デザインでいえば, ランダム化比較試験 や 準ランダム化比較試験 などで多く使われる検定方法です。 実は正規分布効果量の用途 • 結果を示す(効果の大きさ) • メタ分析に用いる – メタ分析の回を参照 • 検出力分析に用いる対応バージョン(chisqtest関数): 365 19 16 13 10 対応バージョン(chitest関数): 365 19 16 13 10 実測値範囲と期待値範囲をもとに、カイ二乗検定(適合性や独立性の検定)を行います。
二標本 t 検定(分散が等しいと仮定) 「グループ1の睡眠増加時間の平均」と「グループ2の睡眠増加時間の平均」で差があるかどうかを検定する方法を紹介する.ここでは 2 つのグループの分散が等しいと仮定して,関数 ttest() を用いて検定を行う.残念ながら、データの受理に失敗しました。 データ入力に誤りがあると思われます。 よくご確認のうえ、もう一度データの入力を行って下さい。 どうしても失敗する時には、こちら側のプログラム上の 不備が原因かも知れませんので、 TOPページ からMS Excelによるデータ処理 入門編 初心者のためのExcel VBAの超簡単な使い方 ユーザーフォームを使ってみよう VBAを使ってグラフと図形を作ってみる
以下の式で検定統計量を計算する。 χ2 0 = m ∑ i=1 ( fi−Ei )2 Ei χ 0 2 = ∑ i = 1 m ( f i − E i ) 2 E i 例題では, χ2 0 =6000 χ 0 2 = 6000 となる。 χ2 0 χ 0 2 は,自由度が m−1−2 m − 1 − 2 の χ2 χ 2 分布に従う (母平均と母分散の推定を行ったため,自由度が 2 2 だけ6 今回、3$有意水準でのr値は4 で、観察されたr値である 346 のほうが大きい つまり、帰無仮説&休み前後で点数に差は無い'が発生する確率は5% 未満であり第7章 順位和検定 数表72 MannWhitneyのU検定のU統計量の分布(片側検定,標本数:N1=6, N2=6) 確率P 0001 0002 0004 0008 0013 0021 0032 0047 0066 0090




統計ソフト情報




T 検定メインページ Ultrabem トップページ
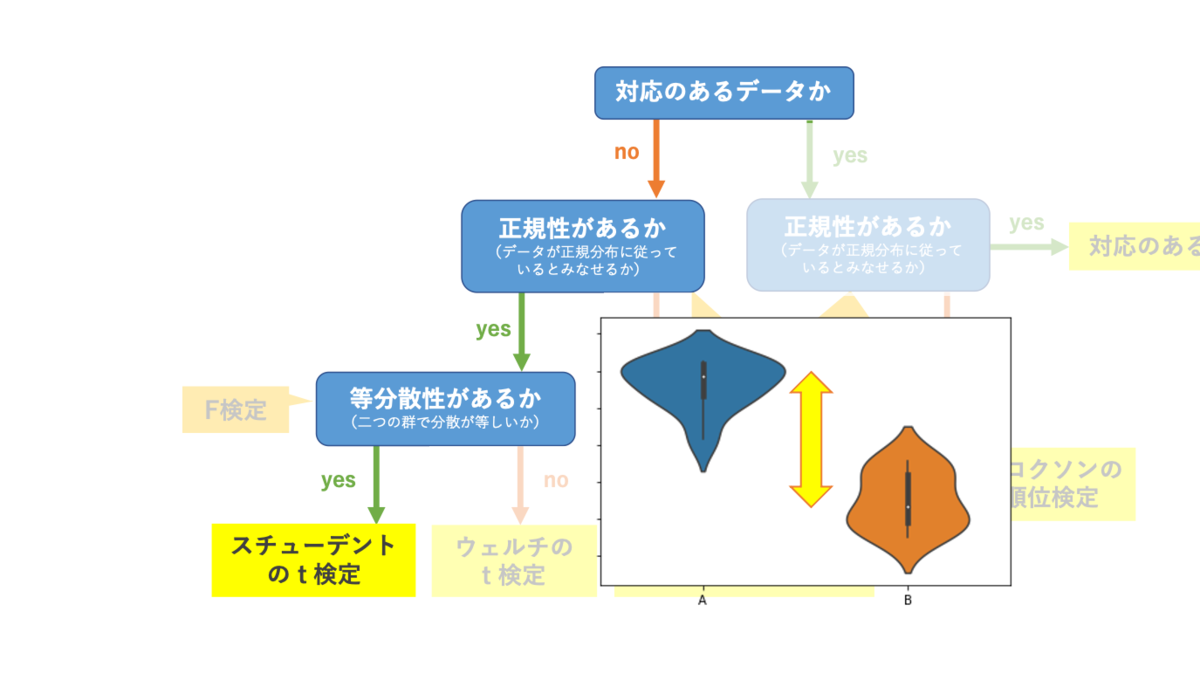
1 原稿作成日: 17年3月31日 検定の選び方: 検定は結論を変え得る! 不適切な検定を故意に選ぶのは不正行為P = ranksum(x,y) は、ウィルコクソン順位和検定の両側値 p を返します。 ranksum は、x および y のデータが、等しい中央値をもつ連続分布からの標本であるという帰無仮説を、その対立仮説に対して検定します。 この検定では 2 つの標本が独立していると仮定します。x と y の長さは異なる場合がマンホイットニーのU検定を行うマクロ マンホイットニーのU検定におけるU統計量と標準Z得点を計算します。 データ数を返す関数length()も用意されています。 標準Z得点は同順位がある場合に対応していません。 Excelワークシートをダウンロード



マン ホイットニー の U 検定 Mann




19 号 マウスのうつ及び 又は不安症バイオマーカー Astamuse
一対の標本による平均の検定」「対応のある2群の平均値差の検定」「データに対応がある場合のt検定」とも呼ばれる を用いる. 1 同一の被験者に対して異なる2つの条件で測定したとき,それぞれの条件下での母集団平均が等しいかどうかの比較を行う'ZEGN °8ÿ»I ÒH A d_ Excel æê&Ô




Title 教育実践によって得られたデータの解析方法 フリー統計ソフトウェアezrの紹介 Author S 杉尾 幸司 宮国 泰史 Citation 高度教職実践専攻 教職大学院 紀要 2 Issue Date Url Pdf 無料ダウンロード



Pythonによる仮説検定の実行方法 データサイエンス情報局
Buchner, 07)やデータ解析環境Rを使って実行することができる (豊田, 09)。 24 効果量(Effect Size)Wilcoxonの順位和検定(マン・ホイットニーのU検定) (原データを用いることができます) 手法の説明 ・使用法 ・in English※後日,マン・ホイットニーのu検定で多重比較するためにも クラスカル・ウォリスの検定をエクセルでやる を記事にしました. これで,「スチューデント化された範囲の表」とかを使わずとも,エクセル




パラメトリック 検定 論文でよく使う統計手法 検定の選び方や一覧のまとめ




統計 クラスカル ウォリス検定 Kruskal Wallis Test こちにぃるの日記
M U = n 1 n 2 2 {\displaystyle m_ {U}= {\frac {n_ {1}n_ {2}} {2}}} σ U = n 1 n 2 ( n 1 n 2 1 ) 12 {\displaystyle \sigma _ {U}= {\sqrt {\frac {n_ {1}n_ {2} (n_ {1}n_ {2}1)} {12}}}} U検定は独立な標本に対する スチューデントのt検定 と同様の状況で用いられ、どちらを用いるのがよいかが問題になる。 コンピュータ が簡単に使えなかった頃は計算の手間がかからないことから一般にU検定が推奨さ4 Erdfelder, Lang, &2つの独立標本でのノン・パラメトリック検定 D を標本間の位置における仮定された差であると指定し(一般的に等質性を検定し,したがって Dは0である),P1P2 を標本間の位置の差であるとするなら,選ばれる対立仮説によって3つの検定が可能である




Ppt 3 群以上の場合 T 検定か多重比較検定か 片側か両側検定かどちらを選ぶ 報告書に記載してください Powerpoint Presentation Id



無相関検定の概要とpythonコード 実践ケモインフォ
比率の差の検定で用いた例も分割表の一種です. 属性の分割数により,k×m分割表と呼びます. 帰無仮説H 0 2つの属性に関連はない(独立である)に対し,次の検定統計量, が自由度(k1)×(m1)のX 2 分布に従うことを利用して検定を行います.上の例では,性別と選択肢(学校,金融機関)の間にはU値は次のようになる。 U値 = 2+2+3 +5 = 125 n 1 ≦かつn 2 ≦なので、 MannWhitney検定表 よりU値がそれ以上極端となる確率Pを求める。 n 1 =6、n 2 =8のときの両側確率P<005となるU値の下側有意点は8である。 計算したU値は8よりも大きいので、P≧005となり帰無仮説を棄却できない。 よって、「大腸がんと胃がんで鎮痛薬Xに効果の違いがある」とはいえない




三輪書店オンラインショップ 真に役立つ研究のデザインと統計処理 統計の論理的なストーリーを理解する



Boxplot 独学で始める統計 データサイエンス



順位和検定について Excel エクセル で学ぶデータ分析ブログ
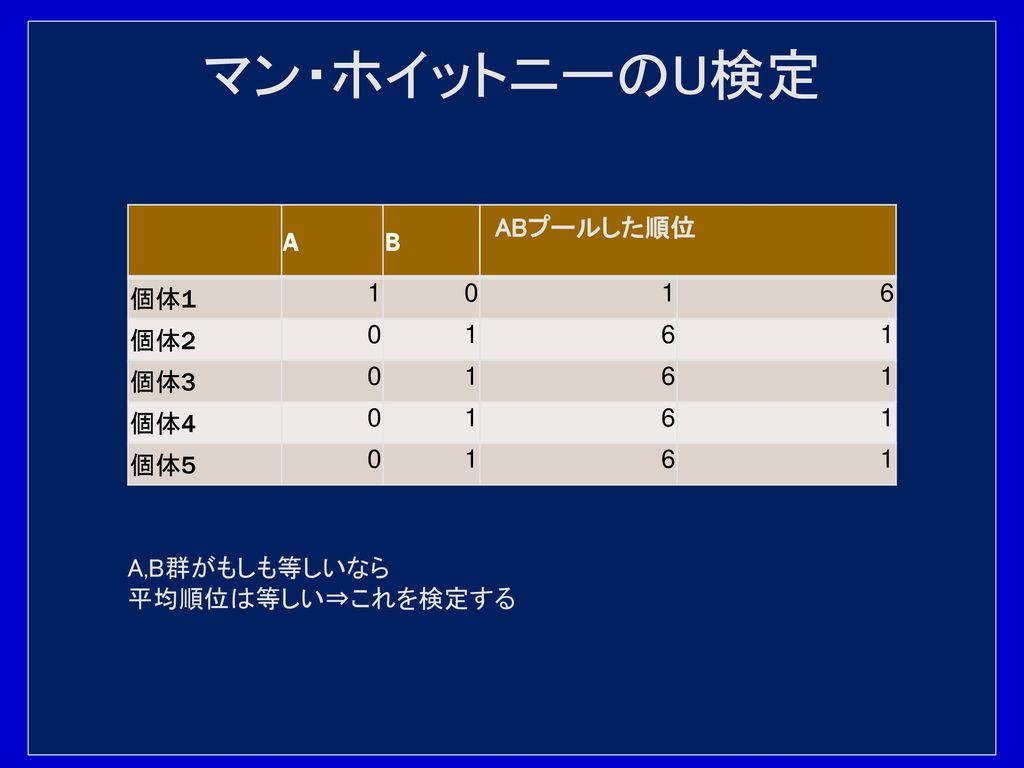



保健統計演習 橋本 Ppt Download




統計解析のソザイヤサン 0から始める初心者向け統計




マン ホイットニー の U 検定 Mann




Stattools 時系列予測および高度な統計分析 Palisade
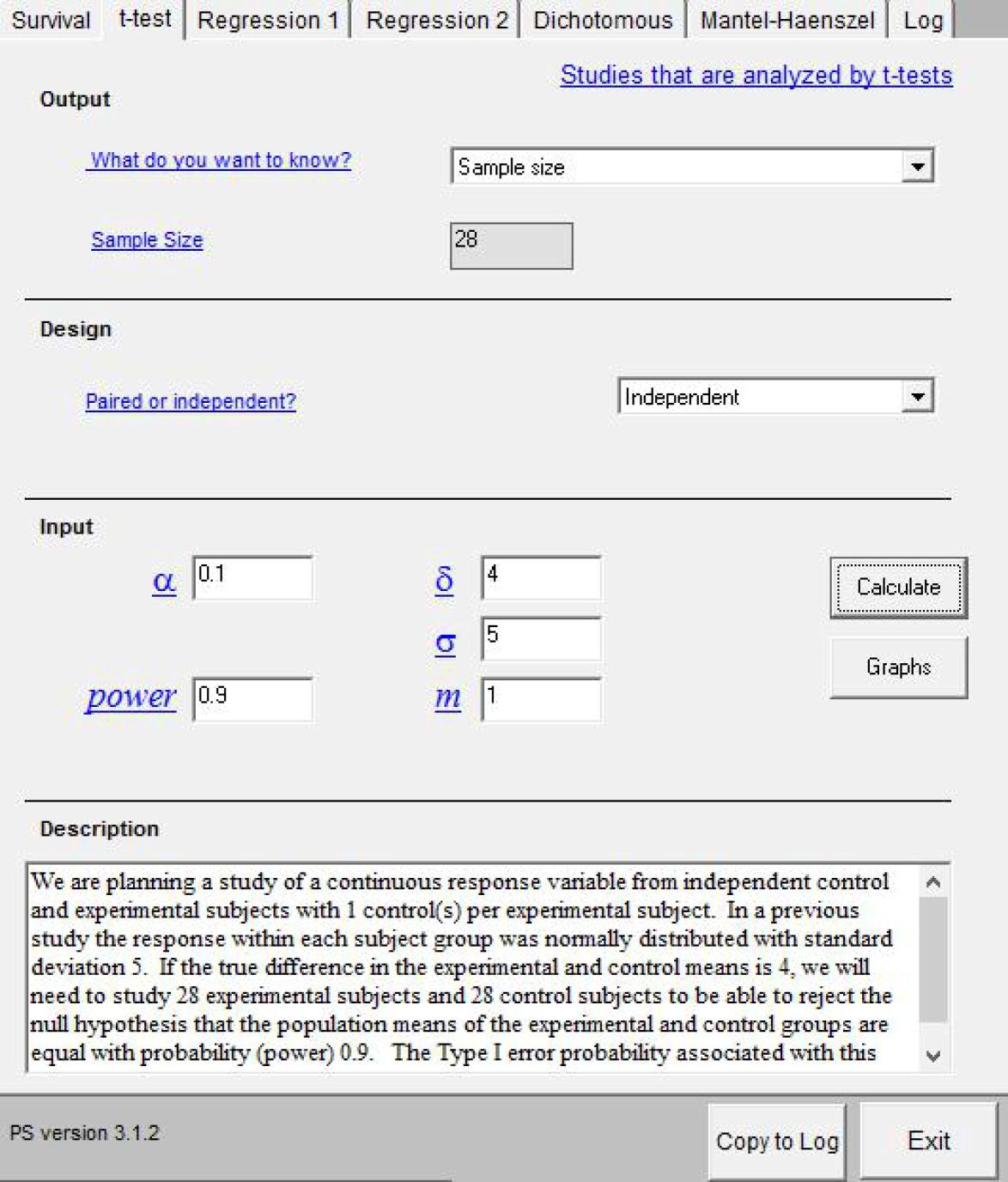



保健 医療研究の進め方入門 Rとezrを用いて 保健学共通特講iv Viiiテキスト Rev 1 0 1




Ezrでpearson ピアソン の相関係数を評価する方法 深kokyu



表計算ソフトで行うwilcoxonの検定 医療情報学




論文を正しく読み書くためのやさしい統計学 改訂第3版 中村 好一 本 通販 Amazon




標準偏差 Wikipedia




最も検出力が高いとされる多重比較 テューキー ウェルシュ法をエクセルで算出する




カーネル密度推定 Wikipedia
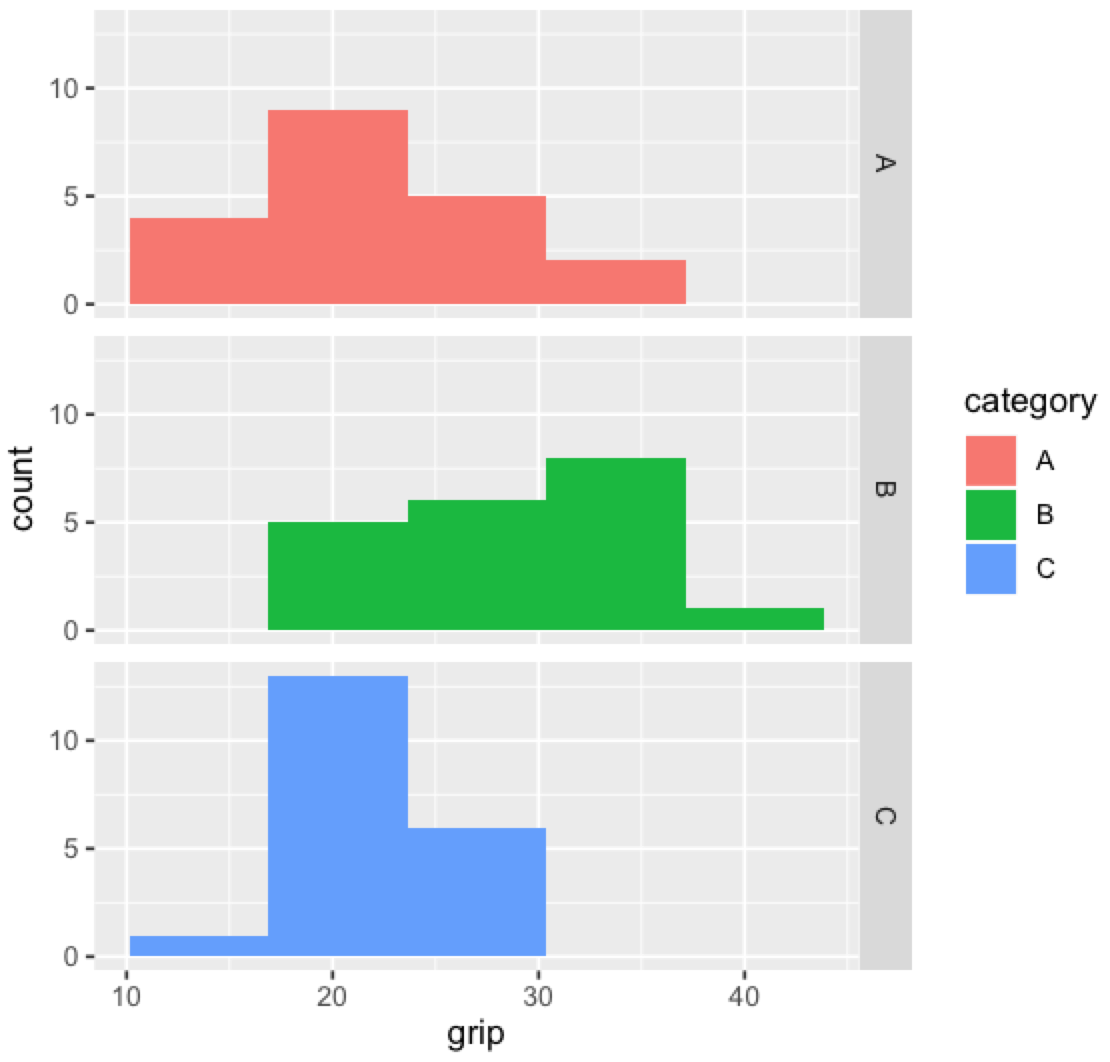



Boxplot 独学で始める統計 データサイエンス




Boxplot 独学で始める統計 データサイエンス




Microsoft Powerpoint 第45回東海循環器画像研究会0529 Pptx Pdf 無料ダウンロード



マン ホイットニー の U 検定 Mann



統計 独学で始める統計 データサイエンス




保健統計演習 1 橋本 永吉 新井 Ppt Download




Spssで比率の区間推定はできるか 統計er




19 号 マウスのうつ及び 又は不安症バイオマーカー Astamuse




ヤフオク 3251 Ssri エクセル統計10




R言語 データの2群比較でやりたいことを全部やっちゃうコードを書いてみた Eiko Programming Note




Wo10 号 慢性ストレスの評価方法 Astamuse



Rでt検定 サルでもわかる機械学習




マン ホイットニーのu検定 少しp値 シティプランナー見習いのブログ




統計学大百科事典 仕事で使う公式 定理 ルール113 Seshop Com 翔泳社の通販




Statmate V 日本スリービー サイエンティフィック



Rでt検定 サルでもわかる機械学習




マン ホイットニー の U 検定 Mann



スチューデントのt検定の概要とpython実装 実践ケモインフォ




マン ホイットニーのu検定のサンプルサイズ計算 統計er



第11章 2つの平均値の比較 Jamoviで学ぶ心理統計




統計解析なんかこわくない 第2版 電子版 医書 Jp




Boxplot 独学で始める統計 データサイエンス



保健統計演習 1 橋本 永吉 新井 Ppt Download




R 独学で始める統計 データサイエンス




マン ホイットニー の U 検定 Mann
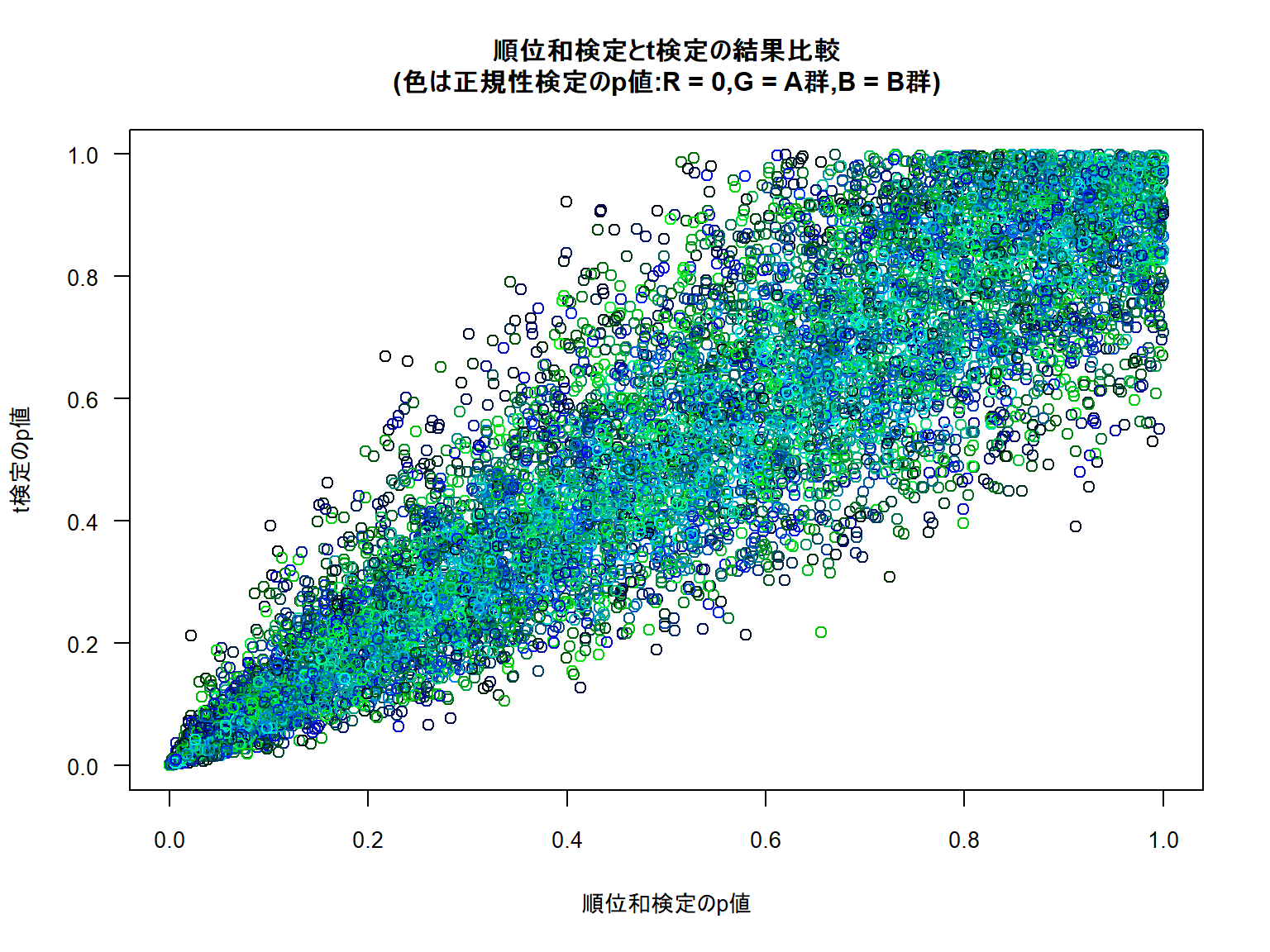



順位和検定について Excel エクセル で学ぶデータ分析ブログ




Spss マンホイットニーのu検定 ウィルコクソンのの符号付き順位和検定 K S Blog
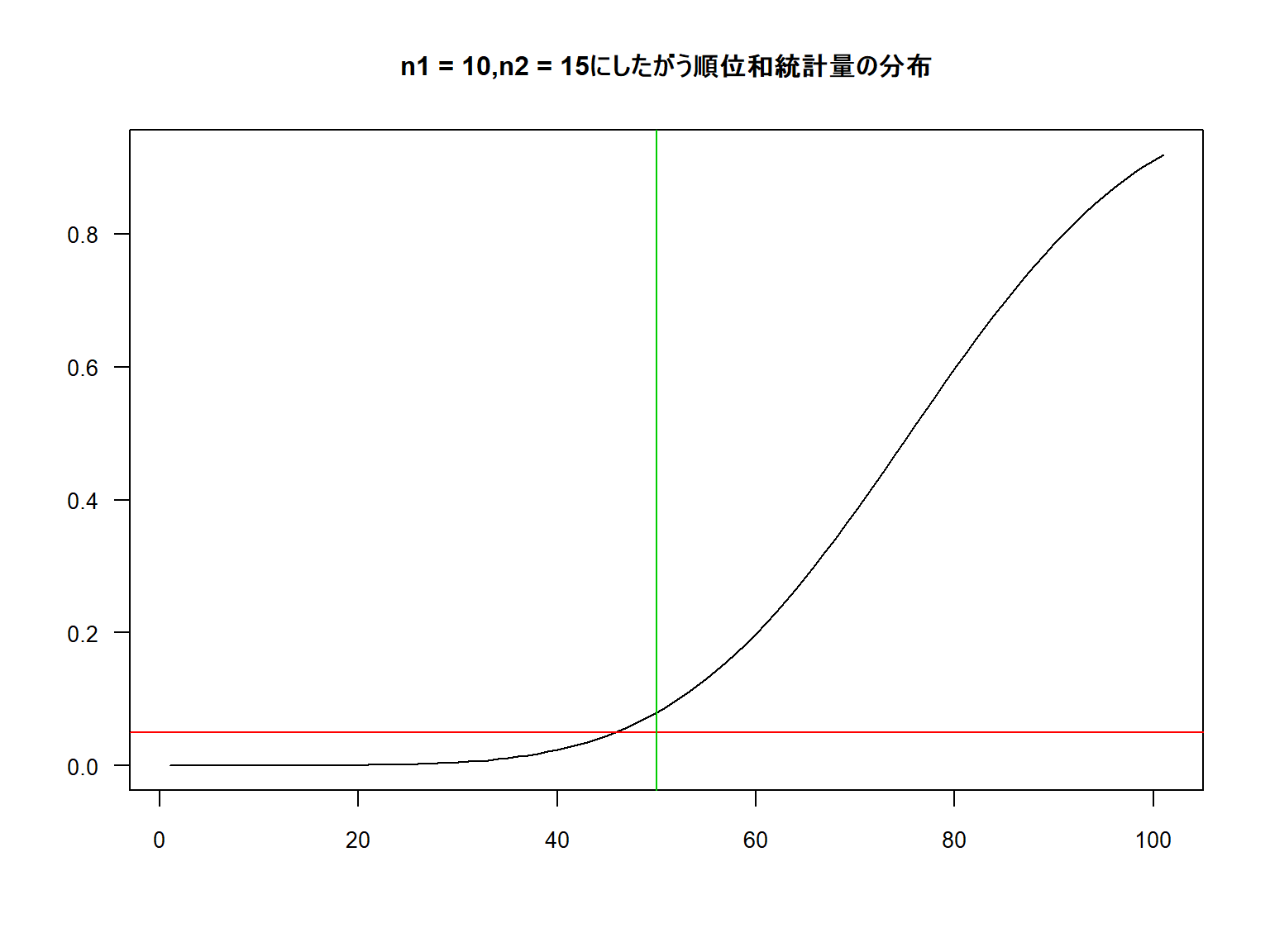



順位和検定について Excel エクセル で学ぶデータ分析ブログ




保健統計演習 橋本 Ppt Download




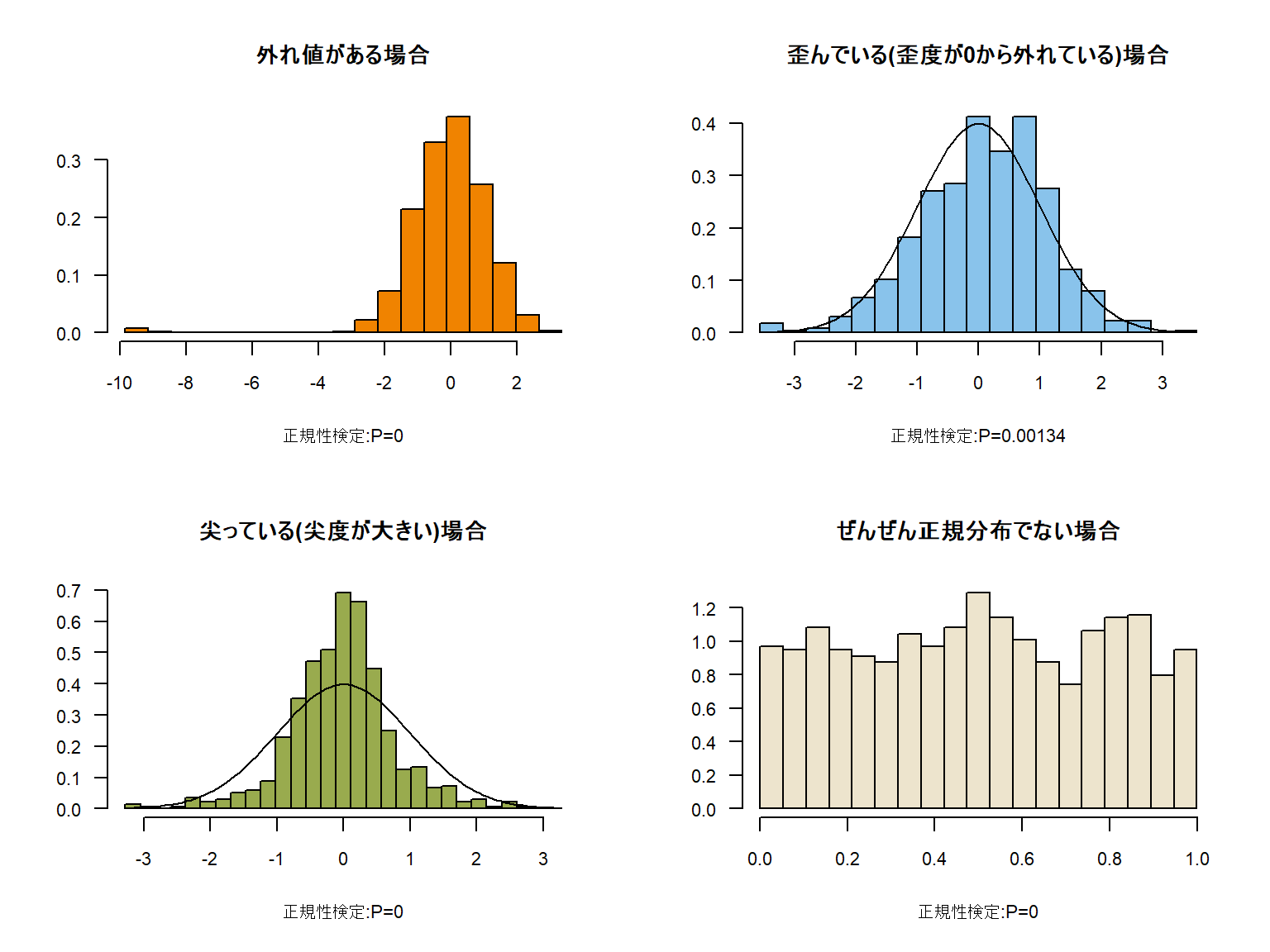
外れ値 Wikipedia




パラメトリック 検定 論文でよく使う統計手法 検定の選び方や一覧のまとめ




最新 中身も確認 心理統計を学べるおすすめ本 入門教科書から実践書まで ランキング Next Topic




Microsoft Powerpoint 第45回東海循環器画像研究会0529 Pptx Pdf 無料ダウンロード




保健統計演習 橋本 Ppt Download




Rでの効果量の計算方法 データ分析エンジニアの自習帳




マン ホイットニー の U 検定 Mann
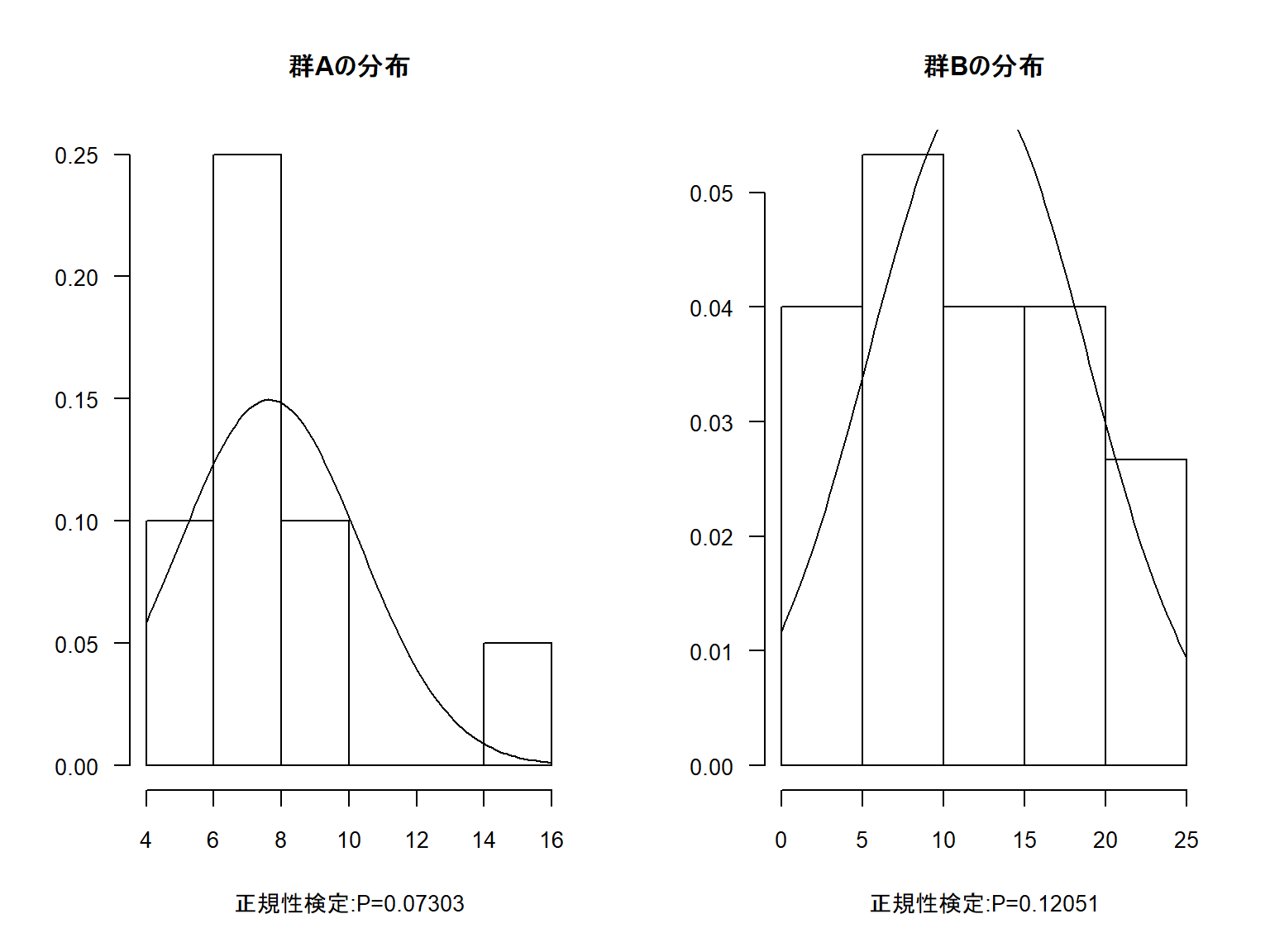



順位和検定について Excel エクセル で学ぶデータ分析ブログ



0 件のコメント:
コメントを投稿